フラクタル(3)

Mathematics and Computingに掲載した「フラクタル1」はJava アプレットを使用していますが、これをJavaScriptで書き直したものを数学とソフトウェアのページの「フラクタル1」に掲載しました。

使い方

「フラクタル記述言語」 (誤ってこのファイルを上書きしてしまったので元に戻したのですが、容量の問題で削除して現在は「フラクタル記述言語: 数学とソフトウェアのメモ２」に掲載しています。これ以外にも説明は「数学とソフトウェアのページ: 数学とソフトウェアのメモ２」に掲載しています)のコードを(1)の領域に書いて(2)の「Draw」ボタンを押すと図形を描くことができます。

(3)のリストから選択すると(1)の領域にサンプルが表示されます。

(2)の領域にエラーなどの状況が表示されますが、詳しくはないのでこれを見てコードを修正するのは難しいと思います。

C#のような形で記述できる「フラクタル7」なども作成しました。「Blockly デベロッパーツール | Google Developers」を使って記述する「フラクタル(Blockly)」も作成しました。式の形で記述できるものをBlocklyに書き直すと、式の方が簡単に書けるのであまり意味がないようなので、単にJavaScriptで記述できるものをBlocklyで書くようになっています。図形を変換するための「変換リスト」をBlocklyで書くようになっています。今後は直接「変換リスト」が書ける機能を追加する予定です。

「フラクタル記述言語: 数学とソフトウェアのメモ２」に掲載したためあまり必要はないのですが以下にも記載しておきます。

フラクタル記述言語

はじめに

ある図形の変形を繰り返した結果できる図形があります。たとえば、

図1 のような線分を

図2 のような数個の線分に変形する操作を繰り返すことによって、

図3 のような図形を描くことができます (「フラクタル数学」p.34、「初めてのフラクタル―数学とプログラミング」p.29)。ここで紹介するものは、このような図形を描画するための言語です。

この言語(今後Fractalということにします)では、図形の情報の集合の間の変換を合成することができます。図形の情報は、図の各(有向)線分の情報です。その集合 f に対して、たとえば f の各要素の線分に対して、 (始点を中心に)長さを2倍にした線分からなる集合 g 考えられます。また、f の各要素の線分に対して、 (始点を中心に)90度回転させた線分からなる集合 h 考えられます。 f に g を対応させる変換を u、f に h を対応させる変換を v とし、このような変換全体の集合を T とします。集合 T の二つの元 u、v に対して、変換 u の結果に対して変換 v を適用した結果を作る変換(変換の合成)を Fractal では u * v と書きます。また、変換 u の結果と変換 v の結果の和集合を作る変換を Fractal では u + v と書きます。

たとえば、

図4 のような線分を、

図5 のような数個の線分に変形する変換は、線分 L から線分 A、B、C、D への変換をそれぞれ a、b、c、d とすると、 Fractalでは図4から図5への変換は、a + b + c + d と表すことができます。また、a + b + c + d を e とすると、図4から図6 (をもうちょっと複雑にしたものを想像してください) への変換は、 e * e * e * e と表すことができます。この結果の図形の情報の集合のそれぞれの要素に対して、線分を描画するには、 e * e * e * e * dl と記述します。 dl は図形の情報の集合のそれぞれの要素に対して、線分を描画するという命令です。すると、

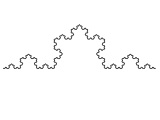
図6のような図形を描画することができます。 Fractalでは、このようにして図形を描画していきます。

使い方

テキストエリアには、あらかじめサンプルが入っていますので、 [Draw]ボタンを押すと、図形が描けるようになっています。サンプルの下から4行めほどにある、

(-10 tm) * (20 tx) * ((frac1 ! 4) **) * dl

が実際に実行された式です。それより上にあるものは、frac1の定義です。定義は「式 = 名前」のように書き、前に定義した名前を後で使うことができます。このように式を「;」で区切って書いていきます。下の先頭に「#」がある行はコメントになります。
式

(-10 tm) * (20 tx) * ((frac1 ! 4) **) * dl

を見てみます。まず、図形が描画される領域は、横方向(x座標) -10 から 10、縦方向(y座標) -10 から 10 という座標になっています。図形の情報の集合の初期状態は、(0,0)-(1,0)の1個の線分になっています。式

(-10 tm) * (20 tx) * ((frac1 ! 4) **) * dl

はこの初期状態に対して

(-10 tm) * (20 tx) * ((frac1 ! 4) **)

という変換を行い、その結果に対して線分を描画するということを表します。 (-10 tm)は始点を中心に線分の長さの -10 倍の長さを移動することを表します。 (20 tx)は始点を中心に 20 倍の長さに拡大することを表します。

((frac1 ! 4) **)

は

frac1 * frac1 * frac1 * frac1

と同じ意味になります。

((frac1 ! 5) **)

などに書き換えてDrawすると、少し複雑な図形を描画することができます。サンプルの中に frac1、frac2、frac3、frac4、frac5、frac6、frac7 が定義されていますので、 frac1 を frac2、frac3、frac4、frac5、frac6、frac7 に置き換えてみると、別の図形を見ることができます。また frac1 * frac2 * frac3 などに置き換えてみることもできます。

上で使った

(-10 tm) * (20 tx) * ((frac1 ! 4) **) * dl

の行の先頭に「#」をつけて、今度は

#(-10 tm) * (20 tx) (fracop1 ! 4) * dl;

の行の先頭の「#」を削除してDrawしてみてください。 frac1 のときと同じ物が描画されると思います。 fracop1 は frac1 と同じものを「関数定義」を使って書いたものです。これは

(-10 tm) * (20 tx) fracop1 fracop1 fracop1 fracop1 * dl

とも

 (-10 tm) * (20 tx) (fracop1 fracop1 fracop1 fracop1) * dl;

とも書くことができます。 (-10 tm) * (20 tx) fracop1 は変換 (-10 tm) * (20 tx) の結果をさらに fracop1 で変換したものを表します。
さらにその下の

((pi/2) tr) * (-10 tm) * (4 tx) * (ti (ftree1 ! 6)) * ft5 * dl
((pi/2) tr) * (-10 tm) * (4 tx) * (ti (ftree3 ! 3)) * ft5 * dl

も同様にやってみてください。

言語の説明

字句

この言語で使う字句は名前、数値、記号で、記号、スペース、タブ、改行が区切りになります。区切りのところでは、適当に改行してかまいません。 #から行の終わりまではコメントです。名前は、アルファベット(大文字・小文字)で始まりアルファベット(大文字・小文字)、数字、アンダースコアが続くものです。数値(実数値)は、普通の実数を表す文字列です。記号は名前と数値定数以外の文字からなるもので

   +  -  *  /  ^  //  %  =  ~~  ~  !  |  ,  ..  :  @
   ?  ==  <>  <  <=  >  >=  ++  **  --  (  )  ;

があります。

全体の記述

この言語の全体の記述は、次のように式を並べたものです。

式; 式; ... 式;

最初の式から最後の式まで、順に実行されます。「式」が「式 = 名前」の形になっているときは、左辺の式は実行されず、名前の定義となります。これ以後、この名前を引用すると、左辺の式の意味になります。

式の型

式には型がある場合があります。型には、

R : 数値(実数)型、
T : 変換型

と、これらを組み合わせた関数型があります。

リスト、組

リストまたは組は、

(式, 式, ... , 式)

と書いたものです。各項目の型が同じ場合はリスト、異なる場合は組となります。

関数

(式関数名) という形の式(関数適用)は、左側の式を引数として、右側の名前で定義されている関数を計算した結果を表します。関数名には、システム関数名とユーザー関数名があります。ユーザー関数名は定義された名前です。関数名のところに次のような式を書くこともできます。

(式 : 名前)
(式 : 名前 @ 型)

これは次の意味になります。

(式1 (式2 : 名前)) := 式2の名前のところを式1で置き換えたもの
(式1 (式2 : 名前 @ 型)) := 式2の名前のところを式1で置き換えたもの

名前の有効範囲は式2の中です。型には R または T を指定することができます。これは名前の型を表します。 (組式)、(式組) という形の式は、次の意味になります。

(組式)
- x1 : X1, x2 : X2, ... , xn : Xn, f : X1->X2->...->Xn->Y
- (x1, x2, ... , xn) f := (x1 (x2 ( ... (xn f) ... ) ) : Y
(式組)
- x : X, f1 : X->X2, f2 : X2->X3, ... , fn : Xn->Xn+1
- x (f1, f2, ... , fn) := ( ... ( (x f1) f2) ... fn) : Xn+1

システム関数名

次のものがあります。

名前	型	意味
tx	R->T	(x tx) は x 倍に拡大する変換
tr	R->T	(x tr) は x だけ回転する変換
tm	R->T	(x tm) は長さの x 倍だけ移動する変換
pr	R->R	(x pr) はステータス領域に数値を出力する(結果は x)
cos	R->R	余弦
sin	R->R	正弦
tan	R->R	正接
acos	R->R	逆余弦
asin	R->R	逆正弦
atan	R->R	逆正接

システム定数名

次のものがあります。

名前	型	意味
ti	T	何もしない変換
to	T	空集合になる変換
dl	T	線分を描画する(結果は空集合になる)
pi	R	円周率

式

式は次のものです。二項演算子と関数適用は左結合です。 (後置単項演算子と二項演算子では二項演算子が優先、 (前置単項演算子と二項演算子では前置単項演算子が優先です。) 不要な括弧は省いてもかまいません。 (結合の順序を変えるために括弧を使うことができます。)

(式式)
(組式)
(式組)
(式二項演算子式)
(式後置単項演算子)
(- 式)
(式 = 名前)
(式 : 名前)
(式 : 名前 @ 型)
(式)

二項演算子

数値

演算子	型	意味
+	R->R->R	加算
-	R->R->R	減算
*	R->R->R	乗算
/	R->R->R	除算
//	R->R->R	商の整数部分
%	R->R->R	剰余
^	R->R->R	べき乗
==	R->R->R	等しい(真のとき1、偽のとき0)
<>	R->R->R	等しくない(真のとき1、偽のとき0)
<	R->R->R	小さい(真のとき1、偽のとき0)
<=	R->R->R	小さいか等しい(真のとき1、偽のとき0)
>	R->R->R	大きい(真のとき1、偽のとき0)
>=	R->R->R	大きいか等しい(真のとき1、偽のとき0)

変換

演算子	型	意味
+	T->T->T	変換の結果の和集合を作る変換
*	T->T->T	変換の合成

リスト、組

演算子	型	意味
..	R->R->L(R)	(x .. y) は x から y までの数値のリスト
!	X->R->L(X)	(x ! n) は n 個の x からなるリスト
?	L(X)->R->X	((x1, x2, ... , xn) ? i) は xn-i
｜	L(X)->(X->Y)->L(Y)	(x1, x2, ... , xn) ｜ f := ( (x1 f), (x2 f), ... , (xn f))
~~	L(X)->(X->X->X)->X型	(x1, x2, ... , xn) ~~ f := (...(x1 (x2 f)) ... (xn f))
,	X->X->L(X)	リストを作る
,	L(X)->X->L(X)	リストの後ろに要素を付け加える
,	X->Y->X*Y	組を作る
,	X1...Xn->Y->X1...Xn*Y	組の後ろに要素を付け加える

その他

演算子	型	意味
~	式	任意の型 (x ~f y) := (x (y f))

単項演算子

後置単項演算子

数値、数値リスト

演算子	型	意味
++	L(R)->R	加算
**	L(R)->R	乗算
--	R->R->R	減算

変換リスト

演算子	型	意味
++	L(T)->T	変換の結果の和集合を作る変換
**	L(T)->T	変換の合成

前置単項演算子

数値

演算子	型	意味
--	R->R->R	減算

式の構文

式
- (式式)
- (組式)
- (式組)
- (式二項演算子式)
- (式後置単項演算子)
- (- 式)
- (式 = 名前)
- (式 : 名前)
- (式 : 名前 @ 型)
- (式)

二項演算子
- +
- -
- *
- /
- ^
- //
- %
- =
- ~~
- ~式
- !
- |
- ,
- ..
- :
- @
- ?
- ==
- <>
- >
- <=
- >=

単項演算子(後置)
- ++
- **
- --

システム関数名
- tx
- tr
- tm
- pr
- cos
- sin
- tan
- acos
- asin
- atan

システム定数名
- ti
- to
- dl
- pi

サンプル

(ti, (y/x atan tr)) ? (x == 0) : x : y = f_tr;
(((x^2)+(y^2))^(1/2) tx) : x : y = f_tx;
(((x^2)+(y^2))^(1/2) tm) : x : y = f_tm;
((x1, y1)f_tr) * ((x1, y1)f_tm) * ((x1, -y1)f_tr) * (((x2-x1), (y2-y1))f_tr) * (((x2-x1), (y2-y1))f_tx) : x1 : y1 : x2 : y2 = fr1;
((0, 0, x1, y1)fr1) + ((x1, y1, 1, 0)fr1) : x1 : y1 = fr2;
((0, 0, x1, y1)fr1) + ((x1, y1, x2, y2)fr1) + ((x2, y2, 1, 0)fr1) : x1 : y1 : x2 : y2 = fr3;
((0, 0, x1, y1)fr1) + ((x1, y1, x2, y2)fr1) + ((x2, y2, x3, y3)fr1) + ((x3, y3, 1, 0)fr1) : x1 : y1 : x2 : y2 : x3 : y3 = fr4;
((1/3), 0, (1/2), (3^(1/2)/6), (2/3), 0)fr4 = frac1;
(0.4, 0.2, 0.6, -0.2)fr3 = frac2;
(0.25, 0.25, 0.75, -0.25)fr3 = frac3;
(0.3, 0.1, 0.7, -0.3)fr3 = frac4;
(0.47, 0, 0.5, 0.47, 0.53, 0)fr4 = frac5;
(0.5, 0, 0.5, 0.33, 0.5, 0)fr4 = frac6;
(0.5, 0.5)fr2 = frac7;
x * frac1 : x = fracop1;
(a tr) * (x tm) * (-a tr) : a @ R : x @ R = ft1;
((a, x)ft1) * (1 tm) * (b tr) * (y tx) * ((-a, x)ft1) : a @ R : x @ R : b @ R : y @ R = ft2;
((a, x, b, y)ft2) + ((-a, x, c, z)ft2) : a @ R : x @ R : b @ R : y @ R : c @ R : z @ R = ft3;
ti + ((((pi/2), (1/2), (pi/6), (3^(1/2)/2), (-pi/3), (1/2))ft3) * x) : x @ T = ftree1;
ti + ((((pi/2), (1/2), (pi/3), (1/2), (-pi/6), (3^(1/2)/2))ft3) * x) : x @ T = ftree2;
((a, x)ft1) + ((-a, x)ft1) : a @ R : x @ R = ft4;
((pi/2), (1/2))ft4 = ft5;
x ftree1 ftree2 : x @ T = ftree3;
(-10 tm) * (20 tx) * ((frac1 ! 4) **) * dl;
#(-10 tm) * (20 tx) (fracop1 ! 4) * dl;
#((pi/2) tr) * (-10 tm) * (4 tx) * (ti (ftree1 ! 6)) * ft5 * dl;
#((pi/2) tr) * (-10 tm) * (4 tx) * (ti (ftree3 ! 3)) * ft5 * dl;